На днях посмотрел ролик Почему на ноль делить нельзя. Тезисно логика автора такая:

1. Чем меньше делитель, чем больше результат.
2. Ноль минимальный из возможных делителей.
3. Результат — самое большое число.
4. Самое большое число — бесконечность.
5. Бесконечность — не число.
6. На ноль делить нельзя по тому, что в результате мы получим не число, хотя планировали получить число.

Если бы мне задали этот вопрос в 10ом классе, я, наверное, так же бы ответил. Но я бы не стал снимать по этому поводу видеоролик и позиционировать себя, как эксперт. Не стал бы кричать «Лож» и сам при этом врать зрителям в лицо.

При чем тут программирование?

Но самое обидное, что так думает не только автор ролика. Но и, например, создатели джаваскрипта. Попробуйте написать alert(1/0); Мы получим: Infinity . Давайте разберемся, что тут не так.

Для начала разберемся с Infinity. В джаваскрипте есть определение и оно очень похоже на определение бесконечности автором ролика. Это некое число, которое больше, чем любое число. Поскольку компьютеры под каждую переменную вынуждены отводить память у этого числа даже есть конкретное значение. Оно больше, чем любое другое число, то есть Number.MAX_VALUE + 1 или 1.7976931348623157e+308 + 1. Нюанс заключается в том, что компилятор не даст нам прибавить к этому числу единицу (просто оставит число таким же) или вычесть единицу из Infinity (опять же останется «бесконечность»). Из-за это особенности авторы языка притворяются, что это действительно бесконечность, а не «то, что вы подумали».
С какой-то версии, правда, ввели еще одну особенность — Infinity>Infinity это true. Так как по логике авторов Infinity — число, которое больше любого числа. Справа — число. Слева то, что всегда больше числа. Понятно. что результат TRUE.

Что делать?

Какой же ответ должен быть с точки зрения математики на пример 1/0? Конечно NaN! NaN — аббревиатура, полная версия это Not a Number, то есть «Не Число». Значение NaN не равно никакому другому числу, включая само NaN. Очевидно, что именно такое «не число» мы и получаем при попытке делить на ноль, а совсем никакую не бесконечность.

В математике есть такой метод, если решение сразу найти не удается, попробуй близкую задачу, которую решить гораздо проще. А потом учти разницу. Например, если меня попросят разделить 100 на 17, то я не смогу того сделать сразу. Мне надо будет сначала решить похожую задачу — разделить 100 на 20. Получится 5. А дальше «учесть ошибку». Ошибка тут это по 3 с каждого вхождения 17 в 100. 3*5 = 15. Итого 100/17 = 5 целых и 15/17. Надеюсь, я смог пояснить метод.

Тут так же. Попробуем взять 1 и поделить на 1. Получится, очевидно 1. Теперь поделим на 0.5. Будет 2. И таким образом мы покажем, что чем меньше число на которое делим, тем больше результат. Тут легко сказать «ну значит ответ бесконечность» и успокоится. Но надо вспомнить, что к нулю можно «подходить» с разных сторон. Если попробовать идти от отрицательных чисел, то будет: 1/(-1) = -1, 1/(-0.5) = -2 .... И так мы получим минус бесконечность. Это можно проиллюстрировать графиком.

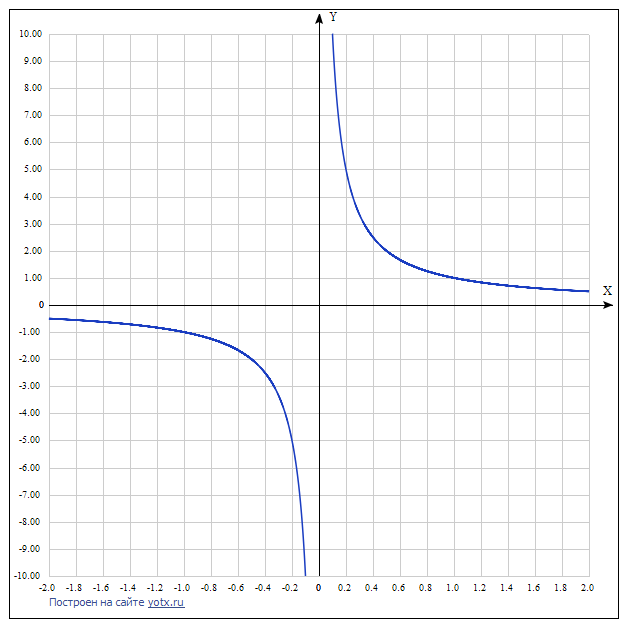
Обратите внимание, что решения вблизи нуля «разлетаются» в разные стороны. Одно вверх, другое вниз. Говоря математическим языком можно это выразить, как «Левый и правый предел расходятся». Мало того, что это разрыв второго рода, так он еще и в разные стороны.

Очевидно, что в такой ситуации мы не можем подобрать такое число, которое хоть как-то близко к решению. Ведь чем ближе число к «решению справа», тем дальше от «решения слева» и наоборот. Это самый, что ни на есть нот-э-намбер.

Вместо вывода

В другом видео нашел более правильное описание всей это ситуации. Ниже привожу его. Не все околонаучные ролики полезны, а некоторые даже вредны.